Without diving too deep
A Mathematical Expression is
“ a finite combination of symbols that is well-formed according to rules that depend on the context”
Symbols can designate numbers (constants), variables, operations, functions, brackets.
As opposed to a statement (formula); an expression is an “incomplete sentence”; It’s more or less a value which could be used in a formula.
Examples of expressions:
1+2
(2+10)/20*(20–90)
5
Fully parenthesized expressions:
Are expressions which “specify precisely which operators apply to which
operands”. eliminating the reliance on operator precedence all together.
Description of algorithm:
- Upon encountering a “(“ : Ignore
- Upon encountering an operand (Number value) : Push onto the operand stack.
- Upon encountering an operator (symbol) : Push onto the operator stack.
- Upon encountering a “)“ : Pop requisite operands , Pop Operator , Push operation result onto Operand stack.
Our implementation :
- Will be in JavaScript.
- We’ll implement the stack ADT using the Array Data-structure, as it has the necessary behavior (.push(), .pop(), .length).
- For simplicity, we’ll assume the following:
- Edge cases such as: “In-complete bracket sequence” are ignored.
- Fully parenthesized sequence. Example: (1+(2*5))
- Single digit numbers. (0–9)
- Basic Binary Operators only (+,-,*,/)
Our Code

We initialize our variables
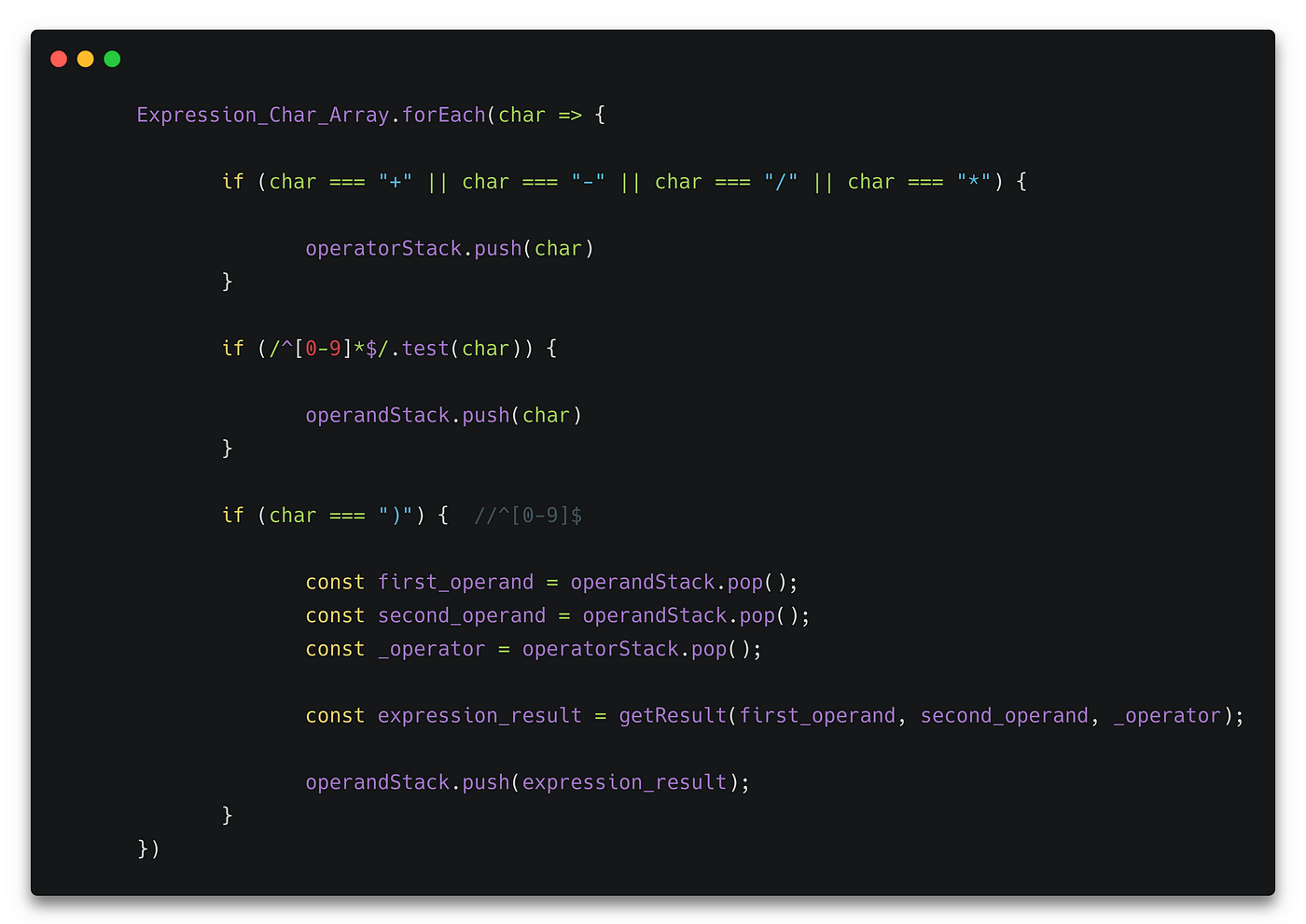
Based on the character; we then perform the steps outlined by the algorithm description above, where we:
- If binary operator: push it onto the Operator Stack.
- If number sequence: push it onto the operand stack.
- If a right “closing” bracket:
- Pop the operand stack twice (because we’re using binary operators).
- Pop the operator stack once.
- Evaluate the expression.
- Push the result onto the operand stack.
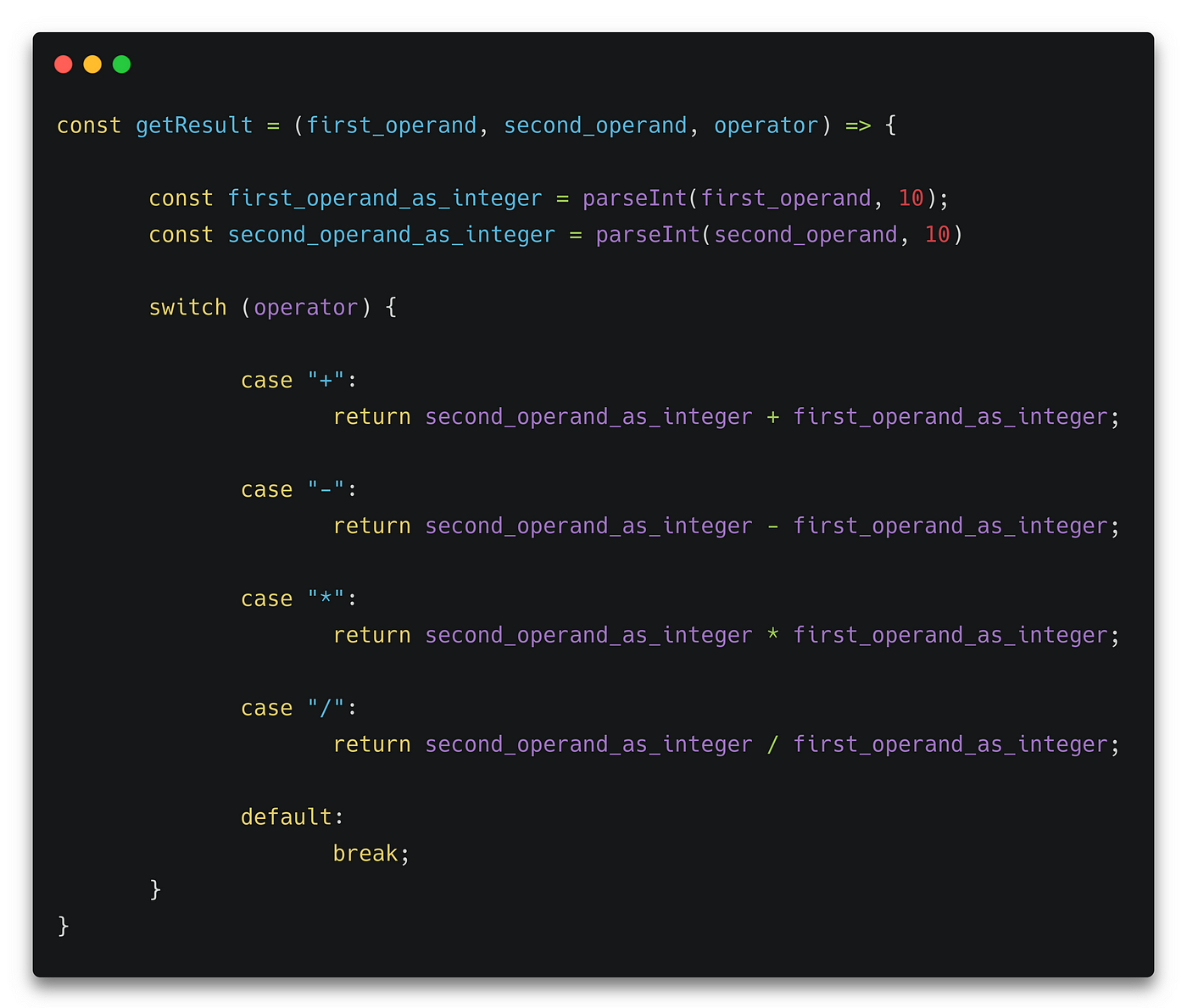
getResult function, used to evaluate a single binary expression, is implemented separately as:
Full Code:
That’s All!
For any inquires, please send me an email at haleesammar@gmail.com.